动态规划是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
由于动态规划并不是某种具体的算法,而是一种解决特定问题的方法,因此它会出现在各式各样的数据结构中,与之相关的题目种类也更为繁杂。
895. 最长上升子序列
题目:
给定一个长度为 N 的数列,求数值严格单调递增的子序列的长度最长是多少。
思路:
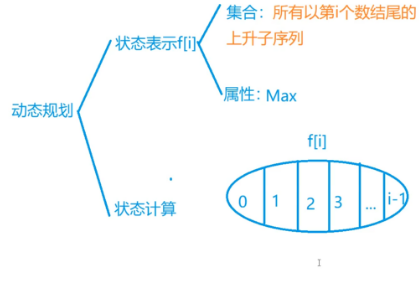
代码:
$O(n^2)$
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n;
int a[N], f[N];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for (int i = 1; i <= n; i ++ )
{
f[i] = 1; // 只有a[i]一个数
for (int j = 1; j < i; j ++ )
if (a[j] < a[i])
f[i] = max(f[i], f[j] + 1);
}
int res = 0;
for (int i = 1; i <= n; i ++ ) res = max(res, f[i]);
printf("%d\n", res);
return 0;
}
q[i]:所有长度为i的上升子序列中结尾最小的数
$O(nlogn)$
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int a[N];
int q[N];//所有不同长度下上升序列结尾的最小值
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
int len = 0;//最大长度
for (int i = 0; i < n; i ++ )
//从q数组(单调递增)中找出小于a[i]的最大的数,q[r],则a[i]是长度为r + 1 的
//上升子序列的最小值,即q[r+1]
{
int l = 0, r = len;
while (l < r)
{
int mid = l + r + 1 >> 1;
if (q[mid] < a[i]) l = mid;
else r = mid - 1;
}
len = max(len, r + 1);
q[r + 1] = a[i];
}
printf("%d\n", len);
return 0;
}
897. 最长公共子序列
题目:
给定两个长度分别为 N 和 M 的字符串A 和 B,求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。
思路:
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main()
{
scanf("%d%d", &n, &m);
scanf("%s%s", a + 1, b + 1); //读字符串不要用 cin
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
{
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
}
printf("%d\n", f[n][m]);
return 0;
}
1017. 怪盗基德的滑翔翼
题目大意:
一排楼,基德可以从任意楼顶往一边滑翔,最多可以在几个楼顶上停歇?
思路:
从前往后和从后往前找最长上升子序列,取最大的
代码:
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n;
int h[N];
int f[N];
int main()
{
int T;
scanf("%d", &T);
while (T -- )
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &h[i]);
int res = 0;
for (int i = 0; i < n; i ++ )
{
f[i] = 1;
for (int j = 0; j < i; j ++ )
if (h[i] < h[j])
f[i] = max(f[i], f[j] + 1);
res = max(res, f[i]);
}
memset(f, 0, sizeof f);
for (int i = n - 1; i >= 0; i -- )
{
f[i] = 1;
for (int j = n - 1; j > i; j -- )
if (h[i] < h[j])
f[i] = max(f[i], f[j] + 1);
res = max(res, f[i]);
}
printf("%d\n", res);
}
return 0;
}
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1149440709@qq.com

