图论 (Graph theory) 是数学的一个分支,图是图论的主要研究对象。图 (Graph) 是由若干给定的顶点及连接两顶点的边所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系。顶点用于代表事物,连接两顶点的边则用于表示两个事物间具有这种关系。
一般问题
848. 有向图的拓扑序列
给定一个 n 个点 m 条边的有向图,点的编号是 1 到 n,图中可能存在重边和自环。
请输出任意一个该有向图的拓扑序列,如果拓扑序列不存在,则输出 −1。
若一个由图中所有点构成的序列 A 满足:对于图中的每条边 (x,y),x 在 A 中都出现在 y 之前,则称 A 是该图的一个拓扑序列。
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n, m;
int h[N], e[N], ne[N], idx;
int d[N];//某个节点的入度
int q[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
//入队列:q[++ tt] = x
//出队列:x =q[hh ++]
bool topsort()
{
int hh = 0, tt = -1;
for (int i = 1; i <= n; i ++ )
if (!d[i])//d中是e[i]
q[++ tt] = i;//队列中存储的是e[i]
while (hh <= tt)//当队列不空
{
int t = q[hh ++];//从队列头部取出一个元素,t是一个idx
for (int i = h[t]; i != -1; i = ne[i])//取出这个元素的所有出度的idx
{
int j = e[i];//将idx转化为e[i]
if (-- d[j] == 0)
q[++ tt] = j;
}
}
return tt == n - 1;
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
for (int i = 0; i < m; i ++ )
{
int a, b;
scanf("%d%d", &a, &b);
add(a, b);
d[b] ++ ;
}
if (!topsort()) puts("-1");
else
{
for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);
puts("");
}
return 0;
}
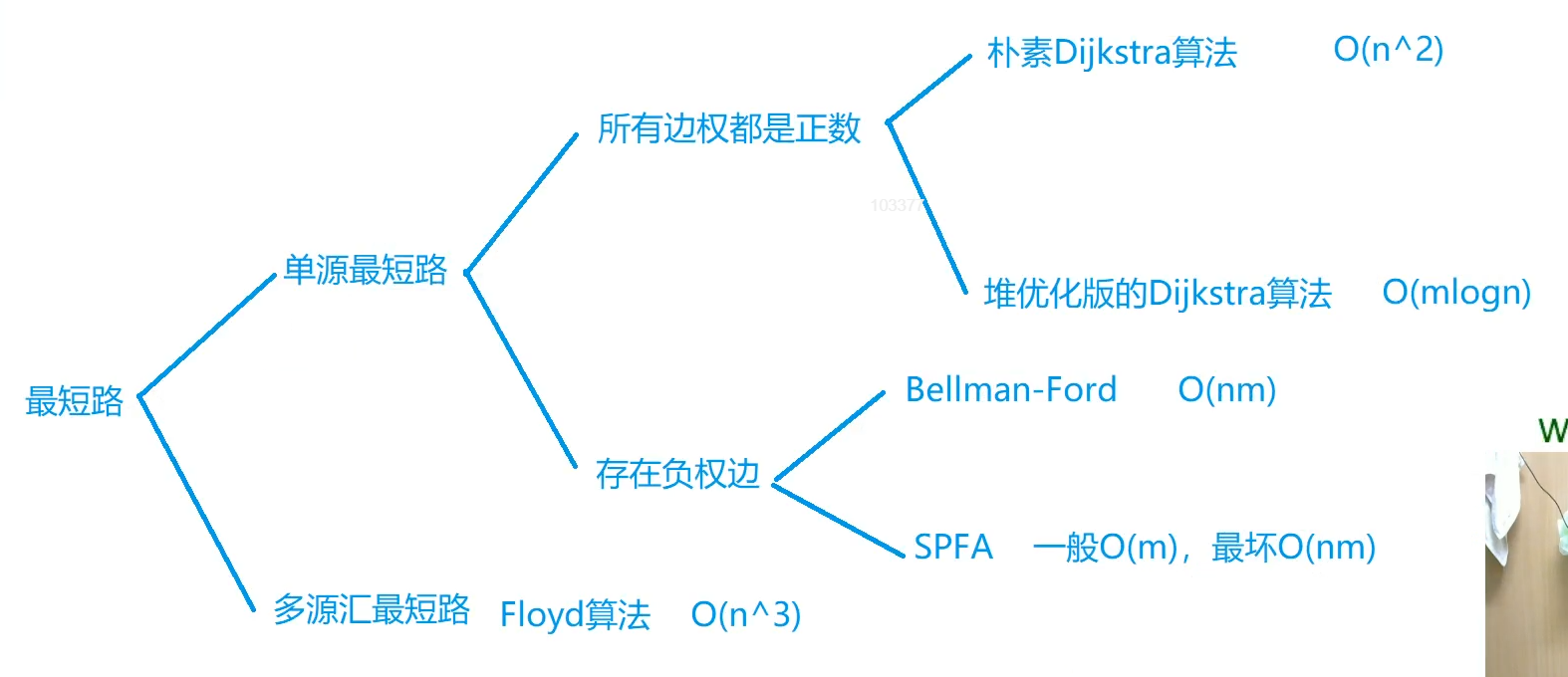
Dijkstra
朴素Dijkstra
int g[N][N]; // 存储每条边
int dist[N]; // 存储1号点到每个点的最短距离
bool st[N]; // 存储每个点的最短路是否已经确定
// 求1号点到n号点的最短路,如果不存在则返回-1
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n - 1; i ++ )
{
int t = -1; // 在还未确定最短路的点中,寻找距离最小的点
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
// 用t更新其他点的距离
for (int j = 1; j <= n; j ++ )
dist[j] = min(dist[j], dist[t] + g[t][j]);
st[t] = true;
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
849. Dijkstra求最短路 I
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 510;
int n, m;
int g[N][N];
int dist[N];
bool st[N];
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n - 1; i ++ )
{
//遍历当前所有未被却认为距离最短的点,即st[i] 为false的点
//选出其中距离源点最近的点的下标,即dist[j]最小的点,用t来记录这个点的下标
//用t来更新其他点到源点的距离,为min(dist[j] , dist[t] + g[t][j]);
//把之前用t记录的点标记为已经确认为的最短距离的点,即另st[t] = true;
int t = -1;
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
for (int j = 1; j <= n; j ++)
dist[j] = min(dist[j], dist[t] + g[t][j]);
st[t] = true;
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
int main()
{
scanf("%d%d", &n, &m);
memset(g, 0x3f, sizeof g);
while (m --)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
g[a][b] = min(g[a][b], c);
}
printf("%d\n", dijkstra());
return 0;
}
Bellman-Ford
int n, m; // n表示点数,m表示边数
int dist[N]; // dist[x]存储1到x的最短路距离
struct Edge // 边,a表示出点,b表示入点,w表示边的权重
{
int a, b, w;
}edges[M];
// 求1到n的最短路距离,如果无法从1走到n,则返回-1。
int bellman_ford()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
// 如果第n次迭代仍然会松弛三角不等式,就说明存在一条长
度是n+1的最短路径,由抽屉原理,路径中至少存在两个相同的点
,说明图中存在负权回路。
for (int i = 0; i < n; i ++ )
{
for (int j = 0; j < m; j ++ )
{
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
if (dist[b] > dist[a] + w)
dist[b] = dist[a] + w;
}
}
if (dist[n] > 0x3f3f3f3f / 2) return -1;
return dist[n];
}
853. 有边数限制的最短路
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出从 1 号点到 n 号点的最多经过 k 条边的最短距离,如果无法从 1 号点走到 n 号点,输出 impossible。
注意:图中可能 存在负权回路 。
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 510, M = 10010;
struct Edge
{
int a, b, c;
}edges[M];
int n, m, k;
int dist[N];
int last[N];
void bellman_ford()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < k; i ++ )
{
//last是备份,上一次的迭代结果
//循环k次,因为多只能走k条路径
//遍历所有的边,e是取出的当前遍历的边
//e.b是e这条边所指向的节点,dist[e.b]是从节点1到e这条边指向的节点的最短路径
//更新dist[e.b]用的是当前值和上一次迭代结果+当前边的权重e.c
//只有当前边e的源点的e.a的dist已经被更新过了,last[e.a]才不是无穷,更新的dist[e.b]才有意义。
//这时候min(dist[e.b],last[e.a] + e.c)取的才是last[e.a] +e.c
memcpy(last, dist, sizeof dist);
for (int j = 0; j < m; j ++ )
{
auto e = edges[j];
dist[e.b] = min(dist[e.b], last[e.a] + e.c);
}
}
}
int main()
{
scanf("%d%d%d", &n, &m, &k);
for (int i = 0; i < m; i ++ )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
edges[i] = {a, b, c};
}
bellman_ford();
if (dist[n] > 0x3f3f3f3f / 2) puts("impossible");
else printf("%d\n", dist[n]);
return 0;
}
spfa
spfa 算法(队列优化的Bellman-Ford算法)
int n; // 总点数
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N]; // 存储每个点到1号点的最短距离
bool st[N]; // 存储每个点是否在队列中
// 求1号点到n号点的最短路距离,如果从1号点无法走到n号点则返回-1
int spfa()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j]) // 如果队列中已存在j,则不需要将j重复插入
{
q.push(j);
st[j] = true;
}
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
851. spfa求最短路
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 impossible。
数据保证不存在负权回路。
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 100010;
int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int spfa()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
spfa是改进版的bellman_ford算法
因为bellman_ford只有在条边的源点的dist更新之后,这条边的汇点的dist才有可能更新
所以只用更新:更新过的节点及其之后所连的点的dist
现在用q队列存储所有已经被更新,但是其后的节点未更新的节点(只要dist更新了,就放到队列中)
每次从q头部取出一个元素q.front设为t,设其st为false,即表示t已经不在队列中了
st[t]是e为t的点是否在队列中,防止队列中出现重复元素
开始遍历t为头部的其后拉链中的所有点
注意dist的[]中是当前节点i的e[i]
如果判断dist[e[i]]>dist[t] + w[i]
即:从点1到点i的距离dist[e[i]]大于从点1到点t的距离dist[t]+从点t到点i的距离w[i]
则更新dist[i]为后者
如果e[i]不在队列中,即st[e[i]]=false,则把e[i]加入队列中,同时设st[e[i]]为true
while (q.size())
{
int t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
return dist[n];
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
int t = spfa();
if (t == 0x3f3f3f3f) puts("impossible");
else printf("%d\n", t);
return 0;
}
852. spfa判断负环
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你判断图中是否存在负权回路。
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 2010, M = 10010;
int n, m;
int h[N], w[M], e[M], ne[M], idx;
int dist[N], cnt[N];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
bool spfa()
{
queue<int> q;
for (int i = 1; i <= n; i ++ )
{
st[i] = true;
q.push(i);
}
while (q.size())
{
int t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n) return true;
cnt[e[i]]是源点到e[i]所经过的边数,为e[t] + 1,t是前一条边的源点
如果一个点的最短路径有n条边,那么有n+1个节点,与题意n个点不符
if (!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
return false;
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
if (spfa()) puts("Yes");
else puts("No");
return 0;
}
Floyd
854. Floyd求最短路
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,边权可能为负数。
再给定 k 个询问,每个询问包含两个整数 x 和 y,表示查询从点 x 到点 y 的最短距离,如果路径不存在,则输出 impossible。
数据保证图中不存在负权回路。
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 210, INF = 1e9;
int n, m, Q;
int d[N][N];
void floyd()
{
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
int main()
{
scanf("%d%d%d", &n, &m, &Q);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
d[a][b] = min(d[a][b], c);
}
floyd();
while (Q -- )
{
int a, b;
scanf("%d%d", &a, &b);
int t = d[a][b];
if (t > INF / 2) puts("impossible");
else printf("%d\n", t);
}
return 0;
}
1471. 牛奶工厂
题目大意:
每个点之间都是单向通道,问是否存在一个点,所有的点都能到这个点
思路1:
O(n^3)
直接Floyd构造出来邻接矩阵,然后看是否有一列全是1
代码1:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110;
int n;
int g[N][N];
int main()
{
cin >> n;
for (int i = 1; i <= n; i ++ ) g[i][i] = 1;
for (int i = 0; i < n - 1; i ++ )
{
int a, b;
cin >> a >> b;
g[a][b] = 1;
}
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (g[i][k] && g[k][j])
g[i][j] = 1;
for (int i = 1; i <= n; i ++ )
{
bool flag = true;
for (int j = 1; j <= n; j ++ )
if (!g[j][i])
{
flag = false;
break;
}
·
if (flag)
{
cout << i << endl;
return 0;
}
}
puts("-1");
return 0;
}
思路2:
O(n)
如果有解的话,解一定唯一
有解 等价于:有且仅有一个点,出度为0
代码2
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110;
int n;
int d[N];
int main()
{
cin >> n;
for (int i = 0; i < n - 1; i ++ )
{
int a, b;
cin >> a >> b;
d[a] ++ ;
}
int cnt = 0, id;
for (int i = 1; i <= n; i ++ )
if (!d[i])
{
cnt ++ ;
id = i;
}
if (cnt == 1) cout << id << endl;
else puts("-1");
return 0;
}
Prim
858. Prim算法求最小生成树
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 510, INF = 0x3f3f3f3f;
int n, m;
int g[N][N];
int dist[N];
bool st[N];
dist[i] 表示i点到已求连通图的最短距离
st[i] 表示i点是否在已求连通图中
进行n次遍历
每次遍历中,在所有的不在已求连通图的点中找出一个距离已知连通图最近的点,记录下标t
如果不是第一次遍历,且找到的距离已知连通图最近的距离是无穷,则返回INF表示不存在最小生成树
否则,将t点的距离加到生成树的边之和res中
把t点加到已知的连通图中,即令st[t] = true;
更新所有点到已知连通图的最短距离,min(dist[j],g[t][j]);
int prim()
{
memset(dist, 0x3f, sizeof dist);
int res = 0;
for (int i = 0; i < n; i ++ )
{
int t = -1;
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
if (i && dist[t] == INF) return INF;
if (i) res += dist[t];
st[t] = true;
for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]);
}
return res;
}
int main()
{
scanf("%d%d", &n, &m);
memset(g, 0x3f, sizeof g);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
g[a][b] = g[b][a] = min(g[a][b], c);
}
int t = prim();
if (t == INF) puts("impossible");
else printf("%d\n", t);
return 0;
}
1140. 最短网络
题目大意:
给一个n*n的方针,a[i][j]代表节点i和j的距离,现在要用光纤连通各个点以建立互联网,问所用光纤的最短距离
思路:
prim算法:由一个中心点不断向外扩张,每次只扩张离已知集合的最短的一条边用邻接矩阵来存储
dist[N]数组存储的是所有点跟已知集合的直接相连的边的最短的距离
代码:
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n;
int w[N][N];
int dist[N];
bool st[N];
int prim()
{
int res = 0;
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n; i ++ )
{
int t = -1;
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
res += dist[t];
st[t] = true;
for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], w[t][j]);
}
return res;
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
cin >> w[i][j];
cout << prim() << endl;
return 0;
}
Kruskal
859. Kruskal算法求最小生成树
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010, M = 200010, INF = 0x3f3f3f3f;
int n, m;
int p[N];
struct Edge{
int a, b, w;
bool operator< (const Edge &W)const
{
return w < W.w;
}
}edges[M];
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int kruskal()
{
1.快速排序
2.枚举每条边a,b,w
如果a,b不连通,(即a,b不在一个集合里面),则将这条边加到集合里面去,a,b的集合合并
sort(edges, edges + m);
for (int i = 1; i <= n; i ++ ) p[i] = i; // 初始化并查集
int res = 0, cnt = 0;
for (int i = 0; i < m; i ++ )
{
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a), b = find(b);
if (a != b)
{
p[a] = b;
res += w;
cnt ++ ;
}
}
if (cnt < n - 1) return INF;
return res;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < m; i ++ )
{
int a, b, w;
scanf("%d%d%d", &a, &b, &w);
edges[i] = {a, b, w};
}
int t = kruskal();
if (t == INF) puts("impossible");
else printf("%d\n", t);
return 0;
}
1141. 局域网
kruskal用结构体来存储,之后要按照边从小到大排序,所以要重载小于号
集合思想
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110, M = 210;
int n, m;
struct Edge
{
int a, b, w;
bool operator< (const Edge &t)const
{
return w < t.w;
}
}e[M];
int p[N];
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) p[i] = i;
for (int i = 0; i < m; i ++ )
{
int a, b, w;
cin >> a >> b >> w;
e[i] = {a, b, w};
}
sort(e, e + m);
int res = 0;
for (int i = 0; i < m; i ++ )
{
int a = find(e[i].a), b = find(e[i].b), w = e[i].w;
if (a != b) p[a] = b;
else res += w;
}
cout << res << endl;
return 0;
}
1143. 联络员
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 2010, M = 10010;
int n, m;
struct Edge
{
int a, b, w;
bool operator< (const Edge &t) const
{
return w < t.w;
}
}e[M];
int p[N];
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) p[i] = i;
int res = 0, k = 0;
for (int i = 0; i < m; i ++ )
{
int t, a, b, w;
cin >> t >> a >> b >> w;
if (t == 1)
{
res += w;
p[find(a)] = find(b);
}
else e[k ++ ] = {a, b, w};
}
sort(e, e + k);
for (int i = 0; i < k; i ++ )
{
int a = find(e[i].a), b = find(e[i].b), w = e[i].w;
if (a != b)
{
p[a] = b;
res += w;
}
}
cout << res << endl;
return 0;
}
二分图
860. 染色法判定二分图
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环。
请你判断这个图是否是二分图。
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010, M = 200010;
int n, m;
int h[N], e[M], ne[M], idx;
int color[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
bool dfs(int u, int c)
{
color[u] = c;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (!color[j])
{
if (!dfs(j, 3 - c)) return false;
}
else if (color[j] == c) return false;
}
return true;
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
while (m -- )
{
int a, b;
scanf("%d%d", &a, &b);
add(a, b), add(b, a);
}
bool flag = true;
for (int i = 1; i <= n; i ++ )
if (!color[i])
{
if (!dfs(i, 1))
{
flag = false;
break;
}
}
if (flag) puts("Yes");
else puts("No");
return 0;
}
861. 二分图的最大匹配
给定一个二分图,其中左半部包含 n1 个点(编号 1∼n1),右半部包含 n2 个点(编号 1∼n2),二分图共包含 m 条边。
数据保证任意一条边的两个端点都不可能在同一部分中。
请你求出二分图的最大匹配数。
二分图的匹配:给定一个二分图 G,在 G 的一个子图 M 中,M 的边集 {E} 中的任意两条边都不依附于同一个顶点,则称 M 是一个匹配。
二分图的最大匹配:所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配,其边数即为最大匹配数。
int n1, n2; // n1表示第一个集合中的点数,n2表示第二个集合中的点数
int h[N], e[M], ne[M], idx; // 邻接表存储所有边,匈牙利算法中只会用到从第一个集合指向第二个集合的边,所以这里只用存一个方向的边
int match[N]; // 存储第二个集合中的每个点当前匹配的第一个集合中的点是哪个
bool st[N]; // 表示第二个集合中的每个点是否已经被遍历过
bool find(int x)
{
for (int i = h[x]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j])
{
st[j] = true;
if (match[j] == 0 || find(match[j]))
{
match[j] = x;
return true;
}
}
}
return false;
}
// 求最大匹配数,依次枚举第一个集合中的每个点能否匹配第二个集合中的点
int res = 0;
for (int i = 1; i <= n1; i ++ )
{
memset(st, false, sizeof st);
if (find(i)) res ++ ;
}
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 510, M = 100010;
int n1, n2, m;
int h[N], e[M], ne[M], idx;
int match[N];
bool st[N];
h[N]后面的拉链是记录的是每个男生的有好感的对象
match[i]是女生i已经匹配了的对象
st[i]是女生i在这一轮有没有被考虑过
逐个遍历男生:
每次遍历时,将所有的女生已经遍历的对象清空
进入find函数,返回这个男生x能不能找到对象
遍历
他所有心仪的对象 j= e[i]
如果这个女生还没有被考虑过,即st[j] = false
那么就让st为true
如果这个女生还没有找到对象,或是他的对象还可以考虑其他女生,则可以将这个女生匹配给x
即返回true,且将match[j]设为x
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
bool find(int x)
{
for (int i = h[x]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j])
{
st[j] = true;
if (match[j] == 0 || find(match[j]))
{
match[j] = x;
return true;
}
}
}
return false;
}
int main()
{
scanf("%d%d%d", &n1, &n2, &m);
memset(h, -1, sizeof h);
while (m -- )
{
int a, b;
scanf("%d%d", &a, &b);
add(a, b);
}
int res = 0;
for (int i = 1; i <= n1; i ++ )
{
memset(st, false, sizeof st);
if (find(i)) res ++ ;
}
printf("%d\n", res);
return 0;
}
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1149440709@qq.com

