贪心算法(英语:greedy algorithm),是用计算机来模拟一个“贪心”的人做出决策的过程。这个人十分贪婪,每一步行动总是按某种指标选取最优的操作。而且他目光短浅,总是只看眼前,并不考虑以后可能造成的影响。
可想而知,并不是所有的时候贪心法都能获得最优解,所以一般使用贪心法的时候,都要确保自己能证明其正确性。
贪心
1660. 社交距离 II
题目大意
在社交距离为R内的牛会被互相感染
R未知
要找到最少的母体数量
输入格式
输入的第一行包含 N。
以下 N 行每行用两个整数 x 和 s 描述一头奶牛,其中 x 为位置,s 为 0 表示健康的奶牛,1 表示染病的奶牛,并且所有可能因传播而染病的奶牛均已染病。
输出格式
输出在疾病开始传播之前已经得病的奶牛的最小数量。
数据范围
1≤N≤1000,
0≤x≤106
输入样例:
6
7 1
1 1
15 1
3 1
10 0
6 1
输出样例:
3
思路
先找到$R_{min}$,它一定 < $min$({两只牛的距离 | 其中两头牛一头被感染一头未被感染 })
要想让母体最少,那么就让R尽可能的大,最大取到$R_{min}$
注:若$R_{min}$的求法是 $R = min$(R,q[i].x - q[i - 1].x),那么$R_{min}$最后求出来的是等于最小的距离,而不是小于
此时我们要将R - 1
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 1010;
int n;
PII q[N];
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ ) cin >> q[i].x >> q[i].y;
sort(q, q + n);
int R = 1e8;
for (int i = 1; i < n; i ++ )
if (q[i].y != q[i - 1].y)
R = min(R, q[i].x - q[i - 1].x);
R -- ;
int res = 0;
for (int i = 0; i < n; i ++ )
if (q[i].y)
{
int j = i + 1;
while (j < n && q[j].y && q[j].x - q[j - 1].x <= R)
j ++ ;
res ++ ;
i = j - 1;
}
cout << res << endl;
return 0;
}
55. 连续子数组的最大和
输入一个 非空 整型数组,数组里的数可能为正,也可能为负。
数组中一个或连续的多个整数组成一个子数组。
求所有子数组的和的最大值。
要求时间复杂度为 O(n)。
数据范围
数组长度 [1,1000]。
样例
输入:[1, -2, 3, 10, -4, 7, 2, -5]
输出:18
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int res = INT_MIN, s= 0;
for(auto x : nums){
if(s < 0)s = 0;
s += x;
res = max(res,s);
}
return res;
}
};
430. 纪念品分组
元旦快到了,校学生会让乐乐负责新年晚会的纪念品发放工作。
为使得参加晚会的同学所获得的纪念品价值相对均衡,他要把购来的纪念品根据价格进行分组,但每组最多只能包括两件纪念品,并且每组纪念品的价格之和不能超过一个给定的整数。
为了保证在尽量短的时间内发完所有纪念品,乐乐希望分组的数目最少。
你的任务是写一个程序,找出所有分组方案中分组数最少的一种,输出最少的分组数目。
输入格式
输入文件包含 n+2 行:
第 1 行包括一个整数 w,为每组纪念品价格之和的上限。
第 2 行为一个整数 n,表示购来的纪念品的总件数。
第 3−n+2 行每行包含一个正整数 Pi,表示所对应纪念品的价格。
输出格式
输出文件仅一行,包含一个整数,即最少的分组数目。
数据范围
1≤n≤30000,
80≤w≤2008,
5≤Pi≤w
输入样例:
100
9
90
20
20
30
50
60
70
80
90
输出样例:
6
分析:
(贪心,排序,双指针) O(nlogn)
直觉上讲,分组的时候应该尽可能让每一组的价值之和大一些。
由此得到如下算法:
- 将所有物品按价值排序;
- 从小到大枚举每个物品,每次给当前物品找一个价值尽可能大的且总价值没有超过上限的“同伴物品”,将两个物品分在一组,这一步可以使用双指针算法优化到 O(n)。
- 这样求出的组数就是最小值。
双指针的i,j分别从头和尾走,只走一遍,所以复杂度为O(n)
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 30010;
int n, m;
int w[N];
bool st[N];
int main()
{
cin >> m >> n;
for (int i = 0; i < n; i ++ ) cin >> w[i];
sort(w, w + n);
int res = 0;
for (int i = 0, j = n - 1; i < n; i ++ )
{
if (st[i]) continue;
while (j >= i && (st[j] || w[i] + w[j] > m)) j -- ;
st[i] = st[j] = true;
res ++ ;
}
cout << res << endl;
return 0;
}
104. 货仓选址
在一条数轴上有 N 家商店,它们的坐标分别为 A1∼AN
现在需要在数轴上建立一家货仓,每天清晨,从货仓到每家商店都要运送一车商品。
为了提高效率,求把货仓建在何处,可以使得货仓到每家商店的距离之和最小。
输入格式
第一行输入整数 N。
第二行 N 个整数 A1∼AN
输出格式
输出一个整数,表示距离之和的最小值。
数据范围
1≤N≤100000
0≤Ai≤40000
输入样例:
4
6 2 9 1
输出样例:
12
思路
- 当n=2的时候,无疑是选在中间任意位置,所以可以排序后两两看成一对,所以要让仓库的左边的商店数量和右面的商店数量相等。
- 所以,仓库应该选在中位数的位置。
代码:
算法1:可以排序
算法2:用nth_element(),把中位数放在a[n / 2]的位置
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int a[N];
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ )cin >>a[i];
nth_element(a, a + n/2, a + n);
int sum = 0;
for (int i = 0; i < n; i ++ )sum += abs(a[i] - a[n / 2]);
cout << sum << endl;
return 0;
}
1478 - 喝饮料
题目:
商店里有n中饮料,第i种饮料有mi毫升,价格为wi。
小明现在手里有x元,他想吃尽量多的饮料,于是向你寻求帮助,怎么样买才能吃的最多。
请注意,每一种饮料都可以只买一部分。
输入样例:
233 6
6 1
23 66
32 23
66 66
1 5
8 5
-1 -1
输出样例:
136.000
思路:
先按照单价从小到大排序,然后从小到大买,如果大于价格,则全买,如果小于价格,则能买多少卖多少
代码:
#include <bits/stdc++.h>
using namespace std;
struct node {
double w, m;
} p[1005];
bool cmp(node a, node b) {
return a.w / a.m < b.w / b.m; //按单价从小到大排序
}
const int N = 10010;
int main() {
int n, x;
while (scanf("%d%d", &x, &n) != EOF) {
if (x == -1 && n == -1)
break;
for (int i = 0; i < n; i++) {
scanf("%lf%lf", &p[i].m, &p[i].w);
}
sort(p, p + n, cmp);
double ans = 0;
for (int i = 0; i < n; i++) {
if (x >= p[i].w) {
ans += p[i].m;
x -= p[i].w;
} else {
ans += p[i].m * x / p[i].w;
break;
}
}
printf("%.3lf\n", ans);
}
}
贪心-区间问题
905. 区间选点
给定 N 个闭区间 [ai,bi],请你在数轴上选择尽量少的点,使得每个区间内至少包含一个选出的点。
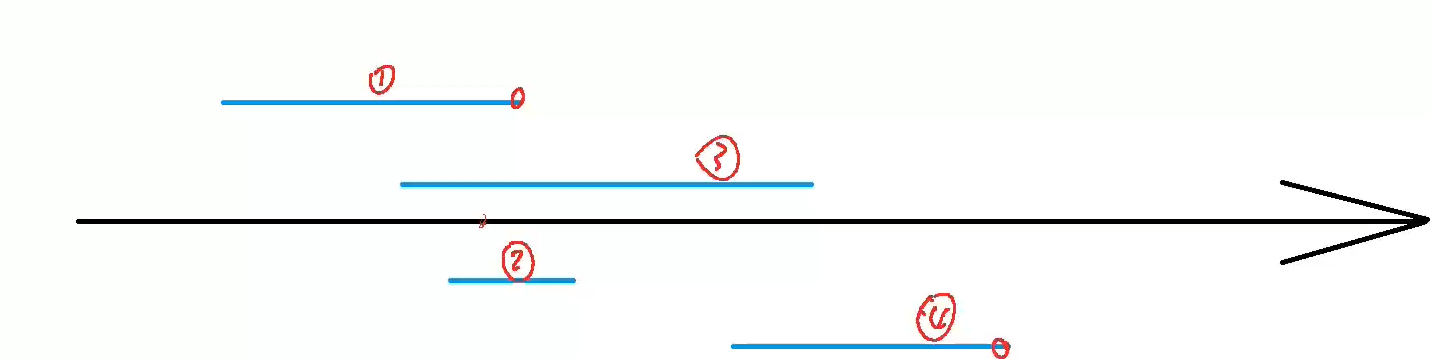
思路:
- 先按照区间右端点排序
- 选当前区间的右端点(该点能覆盖更多的其他区间),将能覆盖的区间排除。找到第一个不能覆盖的区间,此时将答案+1,并更新当前区间为此区间。
#include <iostream>
#include <cstring>
#include <algorithm>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 100010;
int n;
PII p[N];
bool cmp(pair<int, int>a, pair<int, int>b)
{
return a.y < b.y;
}
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ )cin >> p[i].x >> p[i].y;
sort(p, p + n, cmp);
int res = 0, ed = -2e9;
for (int i = 0; i < n; i ++ ){
if(p[i].x > ed){
ed = p[i].y;
res ++;
}
}
cout << res << endl;
return 0;
}
908. 最大不相交区间数量
给定 N 个闭区间 [ai,bi],请你在数轴上选择若干区间,使得选中的区间之间互不相交(包括端点)。
输出可选取区间的最大数量。
思路:
跟问题1完全一样
906. 区间分组
给定 N 个闭区间 [ai,bi],请你将这些区间分成若干组,使得每组内部的区间两两之间(包括端点)没有交集,并使得组数尽可能小。
输出最小组数。
思路:
- 将所有区间的左端点从小到大排序
- 从前往后遍历每个区间,判断能否将当前区间放入现有的某个组,即是否有一个组,其中的所有区间的最右端点在当前区间的左端点的左边,即与当前区间没有交集。(其实判断所有组的最右端点的最小的值是否满足即可)
- 如果存在这样的组,则将当前区间放入这个组中,并更新这个组的最右端点
- 如果不存在这样的组,则开辟新的组,并将当前区间放入这个组中
可以用一个小根堆来记录所有组的最右端点
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 100010;
int n;
PII p[N];
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ ) cin >> p[i].x >> p[i].y;
sort(p, p + n);
priority_queue<int,vector<int>, greater<int>> heap;
for (int i = 0; i < n; i ++ )
{
if(heap.empty() || heap.top() >= p[i].x)heap.push(p[i].y);
else{
heap.pop();
heap.push(p[i].y);
}
}
cout << heap.size() << endl;
return 0;
}
907. 区间覆盖
给定 N 个闭区间 [ai,bi] 以及一个线段区间 [s,t],请你选择尽量少的区间,将指定线段区间完全覆盖。
输出最少区间数,如果无法完全覆盖则输出 −1。
思路:
- 所有的区间按照左端点从小到大排序
- 选择所有能覆盖start的区间中右端点最靠右的区间,并更新start和end
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 100010;
int n;
PII p[N];
int main()
{
int st, end;
cin >> st >> end;
cin >> n;
for (int i = 0; i < n; i ++ ) cin >> p[i].x >> p[i].y;
sort(p, p + n);
int res = 0;
bool success = false;
for (int i = 0; i < n; i ++ ){
int j = i, r = -2e9;
while(j < n && p[j].x <= st){
r = max(r, p[j].y);
j ++;
}
if(r < st){
break;
}
res ++;
if(r >= end){
success = true;
break;
}
st = r;
i = j - 1;
}
if(!success)res = -1;
cout << res << endl;
return 0;
}
源代码
#include <iostream>
#include <cstring>
#include <algorithm>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 110;
int n;
PII p[N];
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ )cin >> p[i].x >> p[i].y;
sort(p, p + n);
int res = 0;
//枚举删除的区间i
for(int i = 0; i < n; i ++){
//sum是去掉第i个区间后,剩余区间最大的覆盖范围
//st是枚举到当合并区间的左端点,ed是枚举到当前合并区间的右端点
int sum = 0, st = -1, ed = -1;
for(int j = 0; j < n;j ++){
if(j != i){
//当前j区间的左端点在当前融合区间的右端点的左边,则可以融合j区间,更新当前融合区间的右端点
if(p[j].x <= ed) ed = max(ed, p[j].y);
//否则开辟一个新的融合区间,并将上一个融合区间的覆盖范围加入到sum里
else{
sum += ed - st;
st = p[j].x, ed = p[j].y;
}
}
}
//加上最后一个融合区间
sum += ed - st;
res = max(res, sum);
}
cout << res << endl;
return 0;
}
110. 防晒
有 CC 头奶牛进行日光浴,第 ii 头奶牛需要 minSPF[i]minSPF[i] 到 maxSPF[i]maxSPF[i] 单位强度之间的阳光。
每头奶牛在日光浴前必须涂防晒霜,防晒霜有 LL 种,涂上第 ii 种之后,身体接收到的阳光强度就会稳定为 SPF[i]SPF[i],第 ii 种防晒霜有 cover[i]cover[i] 瓶。
求最多可以满足多少头奶牛进行日光浴。
输入格式
第一行输入整数 C 和 L。
接下来的 C 行,按次序每行输入一头牛的 minSPF 和 maxSPF 值,即第 i 行输入 minSPF[i] 和 maxSPF[i]。
再接下来的 L 行,按次序每行输入一种防晒霜的 SPF 和 cover 值,即第 i 行输入 SPF[i] 和 cover[i]。
每行的数据之间用空格隔开。
输出格式
输出一个整数,代表最多可以满足奶牛日光浴的奶牛数目。
数据范围
1≤C,L≤2500
1≤minSPF≤maxSPF≤1000
1≤SPF≤1000
输入样例:
3 2
3 10
2 5
1 5
6 2
4 1
输出样例:
2
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1149440709@qq.com

