Pass_02 指令的相关操作

记录一些生疏的、牛批的函数和骗分技巧。

1. 1. count_if
2. 2.count
3. 3.打表法
4. nth_element()

1. count_if

//找有多少个满足lambda 的元素
vector<int> a = {0, 2, 3, 4};
cout << count_if(a.begin(), a.end(), [](int a1)->bool{return a1 <= 2;});
//输出：2

2.count

//找有多少个等于val 的元素
vector<int> a = {0, 2, 3, 4};
cout << count(a.begin(), a.end(), 2);
//输出：1

3.打表法

输出回文素数

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 6e7+10,M=1e8+10;
int n;
int cnt;
int primes[N];
bool st[M];
void get_primes(int n)  
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}
bool is_huiwen(int n)
{
    string s=to_string(n);
    for(int i=0;i<s.size();i++)
        if(s[i]!=s[s.size()-i-1])
            return 0;
    return 1;
}
int main()
{
    freopen("1.txt","w",stdout);
    get_primes(M-1);
    for(int i=0;i<cnt;i++)
        if(is_huiwen(primes[i]))
            cout<<primes[i]<<','; 
    return 0;
}

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int a[]={***}从文件里复制
int main()
{
    int d,f;
    cin>>d>>f;
    for(int i=1;i<=781;i++)
        if(a[i]>=d&&a[i]<=f)
            cout<<a[i]<<endl;
    return 0;
}

nth_element()

nth_element(a, a + k, a + n):将a中第k小的数放在a[k]， k从0开始，小于a[k]的放在a[k]前面，大于a[k]的放在a[k]后面

不用比较函数，将第3+1小的元素4放在a[3]上

#include<cstdio>
#include<algorithm>
using namespace std;
int main()
{
    int n = 9, k = 3;
    int a[10] = {5, 7, 6, 3, 8, 4, 2, 9, 1};
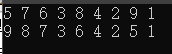
    for(int i = 0; i < n; i ++)printf("%d ",a[i]);
    printf("\n");
    nth_element(a, a + k, a + n);
    for(int i = 0; i < n; i ++)printf("%d ",a[i]);
    printf("\n");
    return 0;
}

用比较函数，将第2+1大的元素7放在a[2]

#include<cstdio>
#include<algorithm>
using namespace std;
int cmp(int a,int b){return a>b;}
int main()
{
    int n = 9, k = 2;
    int a[10] = {5, 7, 6, 3, 8, 4, 2, 9, 1};
    for(int i = 0; i < n; i ++)printf("%d ",a[i]);
    printf("\n");
    nth_element(a, a + k, a + n, cmp);
    for(int i = 0; i < n; i ++)printf("%d ",a[i]);
    printf("\n");
    return 0;
}

最长上升子序列问题

在vector dp里面找到第一个比nums[i]大的位置，并将nums[i]赋给他

auto itr = lower_bound(dp.begin(), dp.end(), nums[i]);
*itr = nums[i];

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 1149440709@qq.com